
Histograma: o que é, como fazer e tabela de frequência!
A estatística é uma ciência da Matemática utilizada para explicar frequências e ocorrências de eventos, seja em estudos observacionais, seja em experimentos de modelagem.
E os resultados obtidos por esses estudos podem ser representados de diversas formas, a partir do uso de variadas ferramentas de análise de dados quantitativos. Um histograma é uma dessas ferramentas, utilizado frequentemente para ilustrar a distribuição de dados estatísticos.
Quer saber como fazer um histograma e como ele pode ser utilizado? Então continue lendo este post!
O que é histograma?
O histograma é uma ferramenta estatística utilizada para a realização de análises e representações de dados quantitativos. Esses dados são agrupados em classes de frequência, de modo que é possível distinguir a forma, o ponto central e a variação da distribuição dos mesmos, além de diversas outras características, como a amplitude e a simetria nessa distribuição.
De maneira resumida, um histograma é considerado um gráfico de frequência, que tem como objetivo ilustrar e representar uma amostra ou população de dados e como estas se encontram distribuídas. Mede, portanto, quantas vezes temos certos valores dentro da distribuição.
Tabela de frequência
Para construir com sucesso um histograma, é preciso que os dados estejam organizados e tabelados. Para tanto, utilizamos a tabela de frequência, na qual listamos nossos dados e suas quantidades.
Essa tabela contém as classes e as respectivas quantidades de aparição de um determinado dado em relação a uma amostra ou população analisada. Vamos considerar uma situação hipotética na qual precisássemos representar, graficamente, a distribuição de altura dos alunos de uma escola. Assim, a melhor maneira de fazer esse exercício é organizar os dados em um histograma.
Entretanto, antes de iniciar a construção do gráfico (histograma) que representará os dados da situação, precisamos montar a tabela de frequência. Nela, inserimos as classes (neste caso, numeradas de 1 a 10), os dados a que correspondem (aqui, a altura em intervalos de 5 centímetros) e a quantidade de alunos de que se encaixam nesses dados, conforme é possível ver na tabela abaixo:
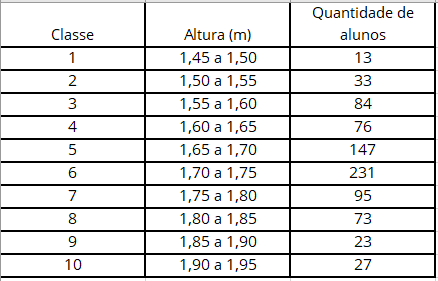
A partir da construção dessa tabela, podemos então partir para a elaboração do nosso histograma.
Como fazer um histograma?
O primeiro passo para montar um histograma é obter sua amostra. No exemplo anterior, temos 802 alunos. A seguir, encontramos os valores máximos e mínimos. Para termos didáticos, podemos dizer que, no nosso exemplo, o valor mínimo é de 1,45 m e o máximo, de 1,95 m.
O próximo passo é calcular a amplitude da nossa série de dados, que mostrará a diferença entre o maior e o menor valor, sendo representada pela letra R (de range, em inglês). Assim, nossa amplitude será representada pela diferença entre a altura do aluno mais alto (1,95 m) e a do aluno mais baixo (1,45 m). Ou seja:
R = maior valor – menor valor
R = 1,95 m – 1,45 m
R = 0,50 m
O terceiro passo é escolher o número de classes que serão utilizadas no nosso histograma. Não existe nenhuma regra específica para essa definição, de modo que o bom senso deve prevalecer. Ou seja, essa quantidade não deve ser nem muito grande, diluindo demasiadamente o gráfico, nem muito pequena, de modo que o histograma fique descaracterizado.
Levando em consideração o dado analisado no nosso exemplo (altura de alunos) e a amplitude (50 centímetros), podemos dividir os dados em 10 classes de 5 centímetros, como foi feito na tabela mostrada anteriormente.
O número de classes também pode variar de acordo com o tamanho da amostra. Assim, podemos utilizar um parâmetro guia, que diz que:
- abaixo de 50 dados de amostra, de 5 a 7 classes;
- entre 50 e 100, de 6 a 10 classes;
- entre 100 e 250, de 7 a 12 classes;
- acima de 250 dados de amostra, de 10 a 20 classes.
O quarto passo é calcular o intervalo das classes. Para isso, dividimos a amplitude pelo número de classes. Como falamos anteriormente, nosso intervalo é calculado pelos 50 cm de amplitude divididos pelas 10 classes, resultando em intervalos de 5 centímetros.
Por fim, montamos a tabela, que no caso do nosso exemplo já foi apresentada no item anterior. A partir de então, é possível montar o gráfico. Em ferramentas como o Excel, a criação do gráfico histograma é simples de ser feita, quando já temos a tabela pronta.
O resultado é apresentado da seguinte maneira:
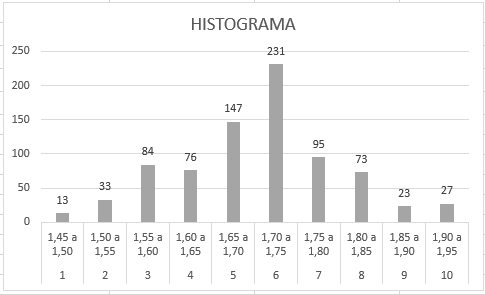
Tipos de histogramas
Podemos classificar os histogramas em diferentes categorias. São elas:
Histograma simétrico
É aquele que apresenta a chamada distribuição normal, no qual os extremos possuem menor frequência e o pico está no centro.
Histograma assimétrico
Neste histograma, temos apenas um pico destacado das demais classes. Representa, geralmente, uma situação na qual a característica de qualidade possui somente um limite de especificação.
Histograma despenhadeiro
Esta categoria ocorre quando certos dados foram eliminados, gerando um “corte” abrupto no gráfico, aparentando um histograma incompleto e inacabado.
Histograma com dois picos
Neste histograma temos a representação de dois picos em diferentes áreas do gráfico. Acontece quando há mistura de dados distintos, como a análise de dois tipos de características diferentes, por exemplo.
Histograma platô
O histograma do tipo platô acontece quando existem diferentes misturas e diferentes distribuições médias, resultando em um gráfico com frequência homogênea entre as classes analisadas.
Histograma “ilha isolada”
Neste tipo de histograma são encontradas algumas classes com frequência semelhante entre si e distintas de todo o resto. Acontece quando há anormalidades no processo de construção do gráfico, decorrentes de falhas ou erros de medição ou tabulação, entre outros.
O histograma é uma das ferramentas básicas de estatística e análise de dados e frequência, podendo ser aplicado em diversas situações, dependendo do objetivo do estudo. Seu entendimento e a capacidade de interpretar seus dados são essenciais para um bom aproveitamento nas questões de estatística nas provas de vestibulares e do Enem!
Depois de aprender o que é um histograma, não deixe de conferir também nosso artigo sobre Função Afim e nossa base de exercícios de Matemática!