Como fazer divisão: passo a passo | Stoodi

Como fazer divisão: passo a passo | Stoodi

Ainda no ensino fundamental, todos aprendemos como fazer divisão de números inteiros, frações, o que é dividendo, divisor, quociente e resto. O procedimento para realizar a operação de divisão sem auxílio de calculadora é relativamente simples, mas contém alguns detalhes que podem ser esquecidos com o tempo. A facilidade de acesso a calculadoras e computadores faz com que pratiquemos pouco o algoritmo da divisão.

É essencial que a prática em multiplicação esteja bem compreendida para facilitar as contas de divisão. Portanto, faça bastante exercícios de multiplicação, para que seja mais fácil fazer divisões.

Estrutura de uma divisão

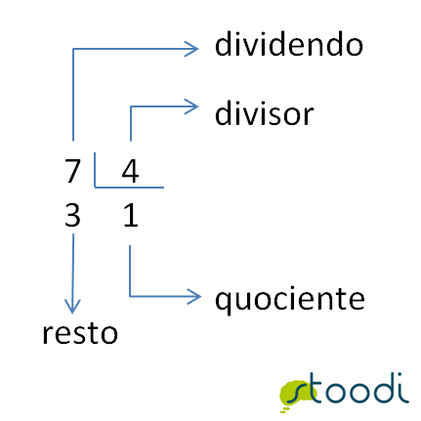
Conforme indicado na imagem acima, a operação de divisão é composta por dividendo, divisor, quociente e resto. Sendo que o dividiendo é o produto do divisor multiplicado pelo quociente e somado ao resto. Para facilitar o seu entendimento, veja no exemplo abaixo:

D = d.q+r

Divisão exata

A divisão é considera exata quando a relação entre o dividendo e o divisor tem o resto igual a 0. Exemplo:

45 / 5 = 9

Resto = 0

Divisão não exata

A divisão é considerada não exata quando ela tem como resto um número maior que 0. Exemplo:

59 / 8 = 7

Resto = 3

Prova real

Para confirmar que o resultado de uma divisão está correto, é possível tirar a prova real. Para isso, basta multiplicar o dividendo pelo divisor. Se o resultado for o mesmo, a divisão foi feita corretamente. Exemplo com os cálculos apresentados acima:

5 x 9 = 45, sem adição de resto, porque foi 0.

8 x 7 = 56 + 3 = 59

Quer ver mais dicas como essa para arrebentar na prova de Matemática do Enem e dos principais vestibulares do Brasil? Então cadastre-se gratuitamente no Stoodi e aproveite.