Fibonacci: quem foi e sequência!
Em vários momentos da sua vida você já deve ter se deparado com sequências numéricas de todos os tipos, não é verdade? Só que existe uma que é alvo da curiosidade humana há muito tempo: a sequência de Fibonacci.
Para que possa incluir esse assunto em seu cronograma de estudos, trouxemos um miniguia com o principal a respeito do matemático que leva o nome da sequência e sua relação com o princípio de ouro. Continue a leitura e confira!
Quem foi Leonardo Fibonacci?
Antes de qualquer coisa, nada mais natural do que conhecermos um pouco mais da trajetória do autor da sequência: o matemático Leonardo Fibonacci. Esse ilustre italiano nasceu em Pisa em 1170, filho de Guglielmo Bonacci, um próspero comerciante da região, e Alessandra Bonacci, que faleceu quando Leonardo tinha apenas 9 anos de idade.
Além de mercador, o pai de Leonardo também era funcionário da alfândega e, por conta disso, levava o menino para fazer viagens a trabalho. Em uma dessas viagens, Leonardo descobriu, por meio de comerciantes orientais, que o sistema hindu-arábico de numeração era muito mais interessante do que os números romanos.
Naquele momento, foi paixão à primeira vista entre Leonardo e a Matemática, o que rendeu a ele uma vida dedicada aos estudos da matéria e descobertas surpreendentes. Aos 32 anos, ele publicou o “Liber Abaci” (Livro de Cálculo), que apresentou à Europa os algarismos hindu-arábicos de 0 a 9 e como eles eram práticos para calcular juros, converter medidas e demais aplicações.
Leonardo escreveu outros livros e foi considerado um dos matemáticos mais brilhantes da Idade Média, sendo que seus feitos foram reconhecidos até pelo Imperador Frederico II. A curiosidade é que o matemático era chamado na verdade de Leonardo de Pisa ou Bigollo. O sobrenome Fibonacci é a abreviação de “fillius Bonacci” (filho de Bonacci), alcunha que foi inventada pelo historiador Guillaume Libri.
O que é a sequência de Fibonacci?
Provavelmente você já deve ter ouvido falar em diversas sequências numéricas por aí, que são uma sucessão infinita de números que obedecem um padrão específico, tal como acontece no caso das fórmulas PA e PG. No entanto, quando se trata da sequência de Fibonacci, você verá uma relação de recorrência bem diferente de outras.
Em seu famoso livro de cálculos, Leonardo se deparou com
uma análise curiosa, em que precisava identificar o crescimento populacional de coelhos no período de um ano. Ele percebeu que cada par de coelhos maduros gerava um par de coelhos jovens e que isso acontecia sucessivamente a cada mês.
Ao analisar a sequência lógica de nascimentos dos coelhos, o matemático percebeu o seguinte cenário:
- 1º mês — um par de coelhos jovens;
- 2º mês — um par de coelhos maduros;
- 3º mês — um par de coelhos maduros e um par de coelhos jovens;
- 4º mês — dois pares de coelhos maduros e um par de coelhos jovens;
- 5º mês — três pares de coelhos maduros e dois pares de coelhos jovens;
- 6º mês — cinco pares de coelhos maduros e três pares de coelhos jovens;
- 7º mês — oito pares de coelhos maduros e cinco pares de coelhos jovens;
- 8º mês — treze pares de coelhos maduros e oito pares de coelhos jovens;
- etc.
Tendo isso em vista, Fibonacci verificou que aquela sucessão de nascimentos formava uma fila numérica representada pelos números: 1, 1, 2, 3, 5, 8, 13, 21 até o infinito. Portanto, ele percebeu que a partir do terceiro elemento, cada número existente seria a soma dos dois antecessores, ou seja, 1+1 = 2, 2+1 = 3, 3 + 2 = 5 e por aí vai.

Do que se trata o Espiral de Fibonacci?
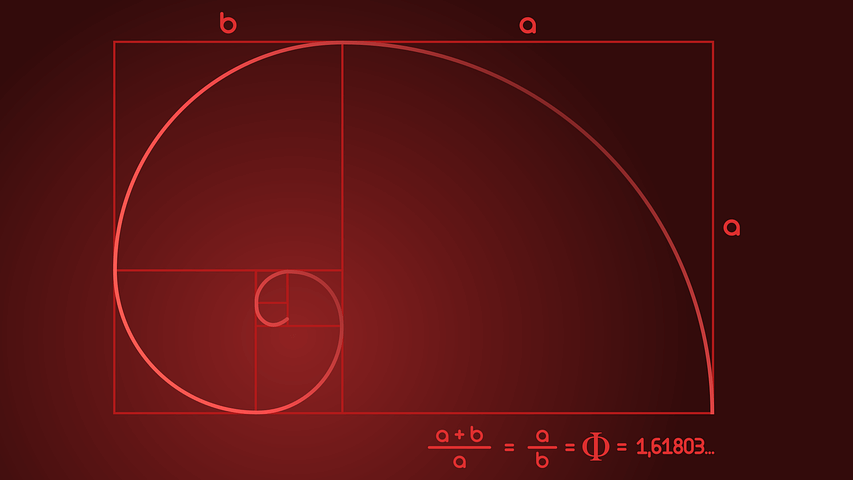
Basicamente, se você utilizar o código Fibonacci e separar em quadrados cujos os lados são equivalentes aos valores apresentados na sequência, é possível criar outra forma em cima disso. Ao pegar ¼ de circunferência de cada quadrante, una-os e terá o que chamamos de espiral de Fibonacci, algo que está presente em diversos elementos da nossa vida.
A formação do arco perfeito seguindo os números pode de ser vista nas sementes da flor de girassol, por exemplo, que formam duas espirais: um em sentido horário com 21 sementes e, naturalmente, o outro em sentido anti-horário com 34 sementes. Nessa observação do girassol, é interessante reparar que ambos os números se fazem presentes na sequência Fibonacci.
Essa espiral pode ser vista em vários outros aspectos da natureza, tais como a concha do caramujo, a tromba do elefante, o rabo do camaleão, o desenho da pinha, além de várias plantas que seguem a lógica matemática de Leonardo. Há ainda teorias de que a sequência seguiria um princípio divino que representa a perfeição do universo.
O que é o Retângulo de ouro?
Você já deve ter notado também que o código Fibonacci forma um retângulo cujas proporções correspondem a cada número da sequência. Essa forma geométrica é estudada por diversos pensadores, até mesmo antes de Leonardo de Pisa, pois há quem diga que essa proporção áurea foi usada em muitas construções antigas, como as pirâmides do Egito e o Partenon na Grécia.
Na matemática, podemos descrever o que é tido como beleza numérica por meio da razão de ouro que é representada pela letra grega phi (φ). O retângulo de ouro serve como base para a arquitetura, os objetos do cotidiano, as artes e até as proporções do corpo humano, como foi retratado na obra “O Homem Vitruviano” de Leonardo da Vinci.
A dízima periódica que corresponde a phi e que é chamada de número de ouro é a sequência 1,61803398… O que é mais surpreendente é que se acharmos a razão de cada número da sequência Fibonacci pelo seu antecessor, os quocientes são muito próximos da proporção áurea, o que torna esse código ainda mais emblemático e significativo.
Para concluirmos, é importante ressaltar que a sequência de Fibonacci é descrita pela fórmula Fn = Fn-1 + Fn-2 e que pode aparecer em qualquer prova por aí, principalmente para mostrar problemas matemáticos que envolvam progressões numéricas.
E aí? O que achou deste texto? Caso tenha gostado do conteúdo que trouxemos cadastre-se gratuitamente no Stoodi e conheça as principais ferramentas do site para ajudar nos seus estudos. Até a próxima!