Função inversa: o que é, exercícios e mais!
Estudar Matemática é uma tarefa importante para quem está querendo ingressar no nível superior. Sendo assim, apresentamos este pequeno guia sobre função inversa. O estudo das expressões algébricas e suas propriedades é uma parte importante do conteúdo cobrado nessa disciplina durante o ensino médio.
Além disso, é comum encontrar questões sobre função e suas variações nos cadernos de Matemática do vestibular, até mesmo nas provas do Enem. Sendo assim, você que está se preparando para esses processos seletivos certamente vai querer estar a par do assunto.
Como dissemos, vamos nos ater aqui à questão da função inversa. Ela é uma derivação da função básica e pode ajudar a encontrar as variáveis de uma equação. Para entender esse conceito, primeiro vamos retomar duas noções necessárias para compreender as funções inversas: o próprio conceito de função e o significado de uma função bijetora.
Vamos lá?
O que é função inversa?
Para iniciar, vale guardar a regra de que nem todas as funções podem ser invertidas, tornando esse um caso bem específico na verificação da resposta desse tipo de equação. Entre outras utilizações, a função inversa serve para derivar uma segunda função da primeira, que a modula inversamente. Você entenderá melhor quando recuperarmos o conceito de função, a seguir.
O que é função?
É uma expressão algébrica tal qual uma equação, composta portanto por letras e números, que propõe uma equivalência em sua expressão, como no exemplo 6 – 1 = x. A diferença é que a função é uma equação que será regulada por um outro elemento, com um valor próprio.
Podemos compreender essa noção a partir da teoria dos conjuntos. Dizemos assim que um conjunto de números está em função de um único elemento de outro conjunto. Isso significa que cada elemento contido nesse primeiro conjunto estará igualmente associado a um único valor que o modula. Podemos representá-lo pela letra y.
O que é função bijetora?
Para que uma função seja efetivamente inversível, é necessário verificar primeiro se estamos lidando com uma função bijetora. Por isso esse conceito é tão importante para o assunto de que estamos tratando. Vamos trabalhar aqui com os seguintes conjuntos hipotéticos C = {a, b, c, d, e} e D = {f, g, h, i, j}.
Utilizamos a notação f para representar função, então poderíamos dizer que f: C → D. Ou seja, o conjunto D está em função de C. No nosso caso, cada elemento do primeiro conjunto está relacionado com uma contraparte do segundo. Diríamos, em termos algébricos, que:
f = { (a, f); (b, g); (c, h); (d, i); (e, j) }
Em nosso exemplo, o oposto também poderia ser aplicado, significando, portanto, que cada um dos elementos do segundo conjunto, D, também admite função com o conjunto C. Neste caso, inverteríamos a expressão e poderíamos dizer também que f: D → C.
Quando isto ocorre, dizemos de uma função bijetora, portanto, que admitiria uma inversa. Na prática, quer dizer que assim como os valores de C determinam cada um dos valores de D, o mesmo pode ser dito sobre em sentido contrário, o valor de D também modula cada um dos valores do conjunto C.
Esse caso nem sempre é possível, pois normalmente as funções funcionam apenas em uma direção, mas, quando ocorre bilateralmente desta forma, podemos dizer primeiro que se trata de uma função bijetora e segundo que ela admite inversão.

Teorema da função inversa
Digamos que a função bijetora de nossos conjuntos C e D é expressa nos seguintes termos:
y = x + 2.
A letra y representa um dos valores do segundo conjunto, enquanto x os elementos do conjunto C. Ou seja, será adicionado ao número de cada um dos itens o valor de 2 para cumprir a função determinada.
Como sabemos que essa é uma função de duas vias, é possível fazer sua inversa. Para tanto, basta usar os princípios algébricos de modo a transformar a expressão para obedecer aos seguintes critérios: f: D → C.
No caso mencionado, basta inverter o algoritmo de lugar e obteríamos a seguinte equação: x = y -2. Essa é a função inversa que estamos buscando. Sobre a notação, se para representar a função ordinária usamos o f, para simbolizar a inversa de uma função: f-¹.
Gráfico da função inversa
A teoria da função inversa pode ser admitida também na análise e interpretação de gráficos. Se for possível inverter a função em questão, então também será possível predizer o formato do gráfico gerado por essas coordenadas.
No caso de uma função inversa, então a reta de x será a mesma de y, só que em formato espelhado. Mas elas não serão sobrepostas, obviamente. Cada linha será especular da outra com relação àquela reta. Portanto, se observar na hora da forma um gráfico espelhado de duas linhas, com o mesmo formato e variações de coordenadas, trata-se de um gráfico de função inversa.
Com o presente artigo, você pôde absorver o essencial sobre a teoria da função inversa. É importante ter em mente o conceito primário de função e o trabalho com equações algébricas. Além disto, conhecer o tipo bijetor dessas fórmulas também será necessário para distinguir se uma função é realmente inversível.
Que tal organizar seus esforços com mais eficiência? Conheça o Plano de Estudos! Com ele você cria rotinas que melhoram seu rendimento e aumentam suas chances de passar no vestibular!
Função inversa: exercícios
Agora que você entende os conceitos básicos de uma função inversa, vamos testar o que foi aprendido com exercícios resolvidos sobre esse conteúdo. No final do texto, temos as respostas das perguntas. Tente por si mesmo antes e confira no final se acertou!
1. (Stoodi) Assinale a afirmativa falsa.
a) Uma função injetora pode não admitir função inversa.
b) Uma função sobrejetora pode admitir função inversa.
c) Uma função bijetora sempre admite função inversa.
d) Uma função bijetora nem sempre admite função inversa.
2. (Stoodi) O diagrama a seguir representa uma função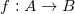

É verdade que:
a) D(f) = {2, 3, 5}, CD(f) = {0, 2, 4, 6, 8, 10} e Im(f) = {4, 6, 10}.
b) D(f) = {0, 2, 4, 6, 8, 10}, CD(f) = {2, 3, 5} e Im(f) = {4, 6, 10}.
c) D(f) = {4, 6, 10}, CD(f) = {0, 2, 4, 6, 8, 10} e Im(f) = {2, 3, 5}.
d) D(f) = {2, 3, 5}, CD(f) = {4, 6, 10} e Im(f) = {0, 2, 4, 6, 8, 10}.
e) D(f) ={0, 2, 4, 6, 8, 10}, CD(f) = {4, 6, 10} e Im(f) = {2, 3, 5}.
Gabarito:
1. c; 2. a.