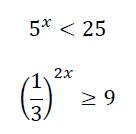
Inequação exponencial
As inequações que envolvem funções exponenciais são chamadas de inequações exponenciais. Por exemplo:
Para sua resolução, procura-se chegar a uma comparação de potências de mesma base para então comparar os expoentes. Utiliza-se a partir daí a informação de que:

Deste fato, decorre que, se a>1:
Se 0<a<1, temos:
Em resumo, na resolução de inequações exponenciais:
- se a base é maior que 1, a desigualdade se mantém.
- se a base está entre 0 e 1, a desigualdade se inverte.
Quer ver alguns exercícios resolvidos pra entender tudinho? Então entra lá no Stoodi.

