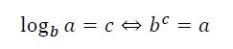
Logaritmo
Apesar de muito temidos entre os estudantes, os logaritmos são um tema relativamente simples, contanto que se entenda sua definição e suas propriedades.
Definição: Ao falarmos sobre logaritmo, temos que ter em mente que estamos falando de expoentes, o que fica claro na relação fundamental:
Aos termos do logaritmo damos os seguintes nomes:
- a: logaritmando
- b: base
- c: logaritmo de b na base a
Logaritmo decimal: Quando a base do logaritmo for 10, o logaritmo é chamado de logaritmo decimal. Neste caso, podemos omiti-la na hora de escrever o logaritmo:
Logaritmo neperiano
O número irracional e=2,718… é chamado de Número de Euler. Quando a base do logaritmo for e, o logaritmo é chamado de logaritmo neperiano. Neste caso, escrevemos:
Os logaritmos neperianos têm diversas aplicações em campos da engenharia, da física e da química.
Assista abaixo à nossa videoaula introdutória sobre logaritmo e acompanhe alguns exemplos e exercícios resolvidos.
Não deixe também de conferir o site do Stoodi, onde você vai encontrar ainda aulas sobre propriedades dos logaritmos, equação logarítmica, função logarítmica e inequação logarítmica, com exemplos resolvidos passo-a-passo.

