
Matemática no Enem: como Proporção pode aparecer?
Dominar o conteúdo de Proporção é muito importante para quem quer mandar bem no Enem. Essa matéria é abordada com frequência na prova de Matemática e suas Tecnologias.
Você vai precisar dela não só para resolver questões específicas, mas também para solucionar outros problemas. A proporção aparece em semelhança de triângulos, em escalas de mapa, em densidade demográfica, entre outros.
A Proporção nada mais é que uma igualdade de razões, ou seja, quando uma razão equivale a outra, elas são proporcionais.
Existem duas propriedades muito importantes que costumam cair bastante no Exame. Vamos revisar?
1ª Propriedade – O produto dos meios é igual ao produto dos extremos
Antes de explicar exatamente a nossa primeira propriedade, precisamos lembrar de alguns nomes.

Agora que já sabemos quem é quem, fica mais fácil entender. Quando o valor dos extremos for igual ao valor dos meios, podemos dizer que eles são proporcionais, pois quando multiplicamos em X, nós estamos verificando se há uma proporção.Vamos ao exemplo para isso ficar mais claro:
“Numa sala nós temos 5 meninos e 3 meninas. Suponhamos que nós queremos aumentar a quantidade de alunos, mantendo a proporção. Para ter 20 meninos, de quantas meninas precisaremos? ”
Se tínhamos 5 meninos e agora temos 20, precisamos aumentar o número de meninas na mesma escola – que nesse caso foi em 4 vezes. Ou seja, passamos de 3 para 12 meninas.
Depois que chegamos a esse resultado, precisamos conferir se ele está correto. Por isso, é importante que você sempre se pergunte, “Mas será que é realmente proporcional?”
Para comprovar, é só aplicar a propriedade e ver se o produto dos meios é igual ao produto dos extremos. Veja:
2ª Propriedade – A divisão dos correspondentes é uma constante
Quando dizemos que uma sequência é proporcional a outra sequência, isso significa que a divisão dos correspondentes é uma constante.
“ x, y e z são proporcionais a a, b e c ”
Nesse caso, os correspondentes são “x e a”, “y e b”, “z e c”.
A constante encontrada é 0,5. Ou seja, pensar em números proporcionais é o mesmo que pensar numa divisão de uma constante.
Quer ver um exemplo de como poderia cair na prova? Então lá vai:
“A soma de três números é 40 e eles são proporcionais a 4, 5 e 11. Que números são esses? ”
Pelos nossos cálculos, nós achamos a constante 2. Como eles são proporcionais, ela será sempre a mesma. Sendo assim, para chegar nesses valores do enunciado, x é 8, y é 10 e z é 22.
Essas são as duas propriedades que mais caem no Exame, mas que tal estudar outras matérias e conteúdos para mandar melhor ainda no Enem? O Stoodi oferece um plano de estudos personalizado para você arrasar nas provas! Confira!
Exercícios de Proporção
(CEFET-SC) Sabendo que x + y = 14, determine x e y na proporção 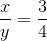
(ENEM 2013) Para se construir um contrapiso, é comum, na constituição do concreto, se utilizar cimento, areia e brita, na seguinte proporção: 1 parte de cimento, 4 partes de areia e 2 partes de brita. Para construir o contrapiso de uma garagem, uma construtora encomendou um caminhão betoneira com 14 m3 de concreto.
Qual é o volume de cimento, em m3, na carga de concreto trazido pela betoneira?