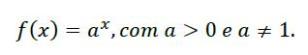
O que são funções exponenciais e como analisar seus gráficos?
O que é uma Função Exponencial?
Funções exponenciais são todas as funções com um número real como base e a incógnita no expoente.
Gráficos
Os gráficos das funções exponenciais são de 2 tipos: crescente ou decrescente, dependendo da base. Se a base for maior que 1, temos uma função crescente e, consequentemente, um gráfico crescente. Se a base estiver entre 0 e 1, temos uma função decrescente e, consequentemente, um gráfico decrescente.

Algumas observações importantes sobre as funções exponenciais:
- As curvas passam pelo ponto (0,1);
- O domínio é o conjunto dos números reais;
- O conjunto imagem é o conjunto dos números reais positivos
No Stoodi, você vai encontrar videoaulas sobre função exponencial com a explicação passo-a-passo dos gráficos acima, além de exemplos de aplicação e vários exercícios resolvidos em nossas aulas de matemática online.