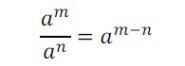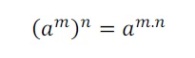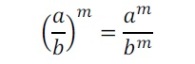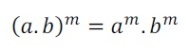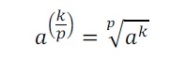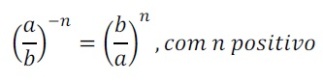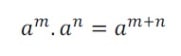
Propriedades da potência: guia completo sobre o tema
As propriedades da potência são poderosas ferramentas na resolução de problemas em diversos campos da ciência. Neste artigo, enunciamos cada uma delas. Vem com a gente aprender tudo sobre o tema!
Produto de potências de mesma base
No produto de potências de mesma base, podemos manter a base e somar os expoentes.
Divisão de potências de mesma base
Na divisão de potências de mesma base, podemos manter a base e subtrair os expoentes.
Potenciação de potência
Na potenciação de potência, podemos manter a base e multiplicar os expoentes.
Potenciação de fração
Na potenciação de fração, o expoente “se distribui” para o numerador e para o denominador.
Potenciação de um produto
Na potenciação de produto, o expoente “se distribui” para os fatores.
Potenciação com expoente fracionário
Na potenciação com expoente fracionário, reescrevemos a base dentro da raiz. O numerador do expoente fracionário será o expoente do radicando e o denominador será o índice da raiz.
Potência com expoente negativo
Na potenciação com expoente negativo, inverte-se a base, e o expoente fica positivo.
Propriedades da potencia: Exercícios
Agora vamos colocar em prática o que você aprendeu sobre propriedades da potência, com alguns exercícios. As respostas estarão no final do texto. Não vale colar, hein?
1) Utilizando apenas propriedades da potenciação, calcule o valor da expressão : 
a.
b.
c.
d.
2) Calculando  , obtemos:
, obtemos:
a.
b.
c.
d.
3) O valor da expressão  é:
é:
a.
b.
c.
d.
e.
Quer tirar todas as suas dúvidas sobre potências, ver exemplos de cada uma das propriedades além de exercícios resolvidos? Acesse já as aulas sobre Potenciação e Radiciação.
RESPOSTAS DO EXERCÍCIO:
1) A
2) D
3 )A