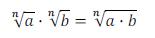
Propriedades da radiciação: entenda de uma vez e domine o tema!
O assunto de hoje é uma ferramenta poderosa na resolução de problemas de matemática. Vamos aprender tudo sobre as propriedades da radiciação.
Produto de raízes de mesmo índice
O produto de raízes de mesmo índice é igual à raiz do produto dos radicandos.
Divisão de raízes de mesmo índice
A divisão de raízes de mesmo índice é igual à raiz da divisão dos radicandos.
Potenciação de raiz
Na potenciação de raiz, podemos manter a raiz e elevar o radicando ao expoente. Pode-se pensar que o expoente que está fora da raiz “entra” na raiz, elevando o radicando.
Simplificação de índice
Se o índice da raiz e o expoente do radicando tiverem fatores em comum, estes podem ser simplificados, como se fossem numerador e denominador de uma fração.
De fato, já foi visto nas propriedades da potenciação que um número, elevado a um expoente fracionário, transforma-se numa raiz: o numerador vira o expoente do radicando e o denominador vira o índice da raiz.
Se fizermos a volta desta transformação, o expoente do radicando vira o numerador da fração e o índice da raiz vira denominador, podendo ser simplificados.
Raiz de raiz
Quando tiramos a raiz n-ésima de uma raiz m-ésima, temos como resultado a raiz n.m-ésima. Em outras palavras, quando fazemos raiz de raiz, mantemos o radicando e multiplicamos os índices.
Quer tirar todas as suas dúvidas sobre radiciação, ver exemplos de cada uma das propriedades além de exercícios resolvidos? Acesse já as aulas sobre Potenciação e Radiciação.



