
Função afim: tudo o que você precisa sobre o assunto!
Um dos primeiros assuntos que todo estudante aprende em Matemática no Ensino Médio é a função afim. E, como ela é a base para aprender os vários outros tipos de funções que vêm depois, é muito importante que você entenda bem esse tópico. Isso inclui entender a teoria e praticar com exercícios de fixação e problemas mais elaborados.
Se você nunca estudou a função afim, ou quer dar uma revisada nos conceitos, prepare-se. Nesse post, vamos retomar tudo o que você precisa saber sobre o assunto!
Função afim: definição
A função afim é toda função polinomial de primeiro grau, isto é, na qual o maior expoente é 1. Pode ser que você conheça a função afim simplesmente como função de primeiro grau.
Lei de formação da função afim
A lei de formação da função afim é expressa na seguinte fórmula:
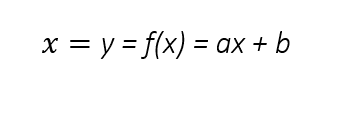
Raiz da função afim
A raiz da função afim é o ponto em que ela atravessa o eixo x, isto é, o ponto em que y = 0. Isso quer dizer que, para descobrir a raiz de uma função afim, basta substituir o y por 0 na fórmula. Ao fazer isso, você tem:
f(x) = ax + b
0 = ax + b
ax = -b
x = -b/a
Dessa maneira, a raiz da função afim é o ponto -b/a no eixo x. As funções de 1º grau têm apenas uma raiz.
Gráfico da função afim

O gráfico da função afim é uma reta crescente ou decrescente. A reta somente não pode ser perpendicular aos eixos x ou y.
Como encontrar dois pontos no gráfico
Como o gráfico da função afim é uma reta, você só precisa de dois pontos para traçá-lo. O primeiro é o ponto da raiz, que você já viu. O segundo é o ponto em que a reta atravessa o eixo y, isto é, em que o x = 0. Nesse ponto, y = b.
f(x) = ax + b
y = a . 0 + b
y = b
Portanto, os dois pontos que você precisa para traçar a reta do gráfico são (-b/a, 0) e (0, b).
Coeficientes da função afim
A função afim tem dois coeficientes: angular e linear.
O coeficiente angular corresponde, na função, ao a. No gráfico, é a tangente do ângulo α (alfa), formado pela intersecção entre a reta da função e o eixo x. Enquanto isso, o coeficiente linear corresponde, na função, ao b. No gráfico, é o ponto de interseção entre a reta da função e o eixo y.
Função afim crescente e decrescente
Você pode determinar a direção da reta do gráfico da função a partir do coeficiente angular, que também é chamado de taxa de crescimento. Quando o coeficiente é maior do que zero, temos uma função afim crescente; quando é menor do que zero, temos uma função afim decrescente.
Tipos de função afim

Existem alguns tipos específicos de função afim, que recebem nomes diferentes. Estamos falando da função linear, identidade e constante. Vamos ver quais são as características de cada uma?
Linear
A função afim é linear quando b = 0, sendo que a ≠ 0. Nesses casos, o gráfico necessariamente passa pelo ponto (0,0). A fórmula da função afim constante também pode ser expressa assim:
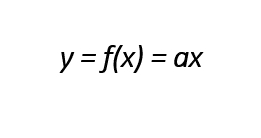
Identidade
A função afim é identidade quando a = 1 e b = 0. Nesses casos, o gráfico necessariamente passa pelo ponto (0,0), e o ângulo α é de 45º. A fórmula da função afim identidade também pode ser expressa assim:
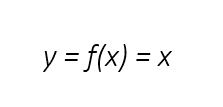
Constante
A função afim é constante quando a = 0. Nesses casos, o gráfico é paralelo ao eixo x. A fórmula da função afim constante também pode ser expressa assim:
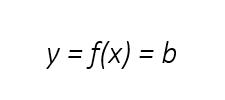
Exercícios de função afim (com resolução)

Agora que você já conferiu os principais conceitos relacionados a função afim, teste seus conhecimentos com os exercícios abaixo!
Exercício 1
Se f(x) = 3x + 2, qual o valor de x para que f(x) = 5?
a. 0
b. 1
c. 2
d. 3
e. 4
Resposta: b
f(x) = 3x + 2
5 = 3x + 2
3x = 5 – 2
3x = 3
x = 1
Exercício 2
Uma função é dada por f(x) = 3x – 6. A raiz dessa função é:
a. 0
b. 1
c. 2
d. 3
e. 4
Resposta: c
f(x) = 3x – 6
0 = 3x – 6
3x = 6
x = 2
Exercício 3
Considere a função f(x) = -2x + 1. Os valores de f(0), f(2), f(-1) e f(5), são, respectivamente:
a. 1, -3, 3, -9
b. -1, 3, -3, -9
c. 1, 5, 3, 11
d. -1, -5, -3, -11
e. 1, 2, 1, 5
Resposta: a
f(x) = -2x + 1
Se x = 0,
f(x) = -2 . 0 + 1
f(x) = 0 + 1
f(x) = 1
Se x = 2,
f(x) = -2 . 2 + 1
f(x) = -4 + 1
f(x) = -3
Se x = -1,
f(x) = -2 . -1 + 1
f(x) = 2 + 1
f(x) = 3
Se x = 5,
f(x) = -2 . 5 + 1
f(x) = -10 + 1
f(x) = -9
Exercício 4
Uma função do 1º grau é dada por f(x) = ax + b. Sabe-se que f(1) = 5 e f(-3) = -7. Essa função é:
a. f(x) = x + 5
b. f(x) = -3x -7
c. f(x) = -3x + 2
d. f(x) = 3x + 2
e. f(x) = x + 4
Resposta: d
f(1) = 5
a . 1 + b = 5
a + b = 5
f(-3) = -7
a . -3 + b = -7
-3a + b = -7
Montando o sistema
a + b = 5
3a – b = 7 (invertendo -3a + b = -7)
4a = 12
a = 3
Se a + b = 5, e a = 3, então:
3 + b = 5
b = 5 – 3 = 2
Assim, a função é:
f(x) = 3x + 2
Depois desses exercícios, você já está pronto para encarar os problemas mais elaborados sobre função afim, como os que são propostos no Enem e nos vestibulares.
Lembre-se de que os conceitos que você viu aqui serão úteis para entender melhor as funções quadráticas (funções de 2º grau) e outros assuntos que estão relacionados. Por isso, não vale partir para o assunto seguinte sem, antes, tirar todas as suas dúvidas sobre função afim!
Quer praticar ainda mais? Então, cadastre-se gratuitamente no Stoodi e tenha acesso a listas completas de exercícios de Matemática, com resolução em vídeo: