
Expressões numéricas: o que são, como resolver e mais!
Todos os conteúdos para o vestibular têm a sua devida importância, mas podemos dizer que alguns deles são ainda mais fundamentais por atuarem como base para a construção de todo o conhecimento ao longo dos estudos. Um desses temas é, sem dúvidas, o de expressões numéricas, algo extremamente recorrente no Enem e vestibulares concorridos!
Frequentemente negligenciado por parecer muito simples, esse assunto pode ser bastante complexo em questões de vestibulares e representa uma importante ferramenta para a resolução dos mais diversos tipos de problemas. Por isso, compreender o seu raciocínio é essencial para todos os vestibulandos!
Continue a leitura e aprenda mais sobre as expressões, seus tipos, formas de resolução e muito mais. Assim, você ficará craque nesse assunto e poderá avançar em seus estudos da Matemática!
O que são expressões numéricas?
Expressões numéricas são, em linguagem simples e compreensível, aglomerados de operações básicas da matemática que, juntas, fazem sentido para a resolução de um determinado problema ou exercício.
Nos vestibulares, elas dificilmente estarão dispostas diretamente em sua forma numérica. A maioria dos exercícios das provas nos apresenta um determinado problema no enunciado e, a partir do que está sendo contado, extraímos as informações necessárias para montar a operação.
Por conta disso, a compreensão das expressões numéricas também está muito relacionada com a interpretação de texto, outra habilidade que deve ser trabalhada duramente ao longo do ano e jamais negligenciada por parte dos vestibulandos. Fique de olho!
Ordem das operações
O primeiro passo para mandar bem nesse tipo de exercício é saber a ordem que as operações seguem em uma resolução. É isso mesmo! Em uma expressão numérica, há uma certa hierarquia que devemos seguir na hora de encarar o problema. No entanto, não se preocupe, porque é tudo bem simples e intuitivo.
A ordem que deve ser seguida é essa:
- radiciação e potenciação;
- multiplicação e divisão;
- adição e subtração.
Além disso, há uma outra ordem que deve ser respeitada no que diz respeito aos elementos da expressão:
- primeiro é resolvido o que está dentro dos parênteses ( );
- depois, é o momento dos colchetes ;
- por fim, são resolvidas as operações dentro das chaves { }.

Como resolver expressões numéricas?
Agora, chegou o momento de descobrirmos o passo a passo para resolver esse tipo de problema. A primeira dica que podemos oferecer é sempre respirar fundo, ler o exercício com calma e grifar todos os elementos que você julgar fundamentais para a resolução.
Entender aquilo que o problema pede é fundamental para a sua resolução. Caso a operação não tenha sido dada e precise ser montada, é hora de perceber o que está sendo perguntado e, a partir daí, anotar a informações em forma numérica.
A seguir, veremos qual é o caminho para a resolução correta desse tipo de exercício!
Sem fração
Imagine a seguinte expressão e resolva-a seguindo os passos dados em nossa resolução:
10 + { 20 – }
O primeiro passo é resolver a divisão que se encontra dentro dos parênteses, elemento priorizado nesses casos. Em seguida, novamente nos parênteses, resolvemos a parte da soma.
Em seguida, o objetivo é resolver tudo o que se encontra dentro dos colchetes. Mais uma vez, a multiplicação é priorizada, enquanto as operações de mais e menos vêm em seguida, na ordem que o aluno preferir resolvê-las.
Por fim, é chegada a hora de eliminar as chaves e fazer a operação final. Durante todo o processo, é essencial que o estudante esteja sempre atento aos jogos de sinais, respeitando as regras para mantê-los positivos ou negativos. Nesse caso, o resultado final da expressão é -31.
Com fração
No caso das frações, seguimos exatamente a mesma lógica vista no exercício anterior. Nada muda, e a ordem de resolução permanece sendo com as operações de radiciação e potenciação, seguida de multiplicação e divisão e terminando com a adição e a subtração.
No caso das potenciações e raízes, a dica é sempre eliminar esse tipo de operação o quanto antes, aplicando as devidas propriedades nas frações. Depois, basta seguir a ordem normalmente, resolvendo a expressão e gabaritando todas as questões que aparecerem em seu caminho!
Exercícios de expressões numéricas
E agora, que tal colocarmos toda essa teoria em prática? Confira alguns exercícios de expressões numéricas e saiba como eles podem aparecer na sua prova! Tudo pronto? Então, vamos lá!
UEL (Paraná)
Considere dois números inteiros, a e b, consecutivos e positivos. Qual das expressões abaixo corresponde necessariamente a um número par?
a) a + b
b) 1 + ab
c) 2 + a + b
d) 2a + b
e) 1 + a + b
Resposta: E
UNAERP (São Paulo)
Analisando as expressões:
I. :(–2/3)
II. (+2 – 3 + 1):(–2+2)
III. (+4–9):(–5+3)
IV (2–3+1):(–7)
Podemos afirmar que zero é o valor de:
a) somente I, II e IV
b) somente I e III
c) somente IV
d) somente II e IV
e) somente II
Resposta: C
ENEM
Uma pesquisa realizada por estudantes da Faculdade de Estatística mostra, em horas por dia, como os jovens entre 12 e 18 anos gastam seu tempo, tanto durante a semana (de segunda-feira a sexta-feira), como no fim de semana (sábado e domingo). A seguinte tabela ilustra os resultados da pesquisa.
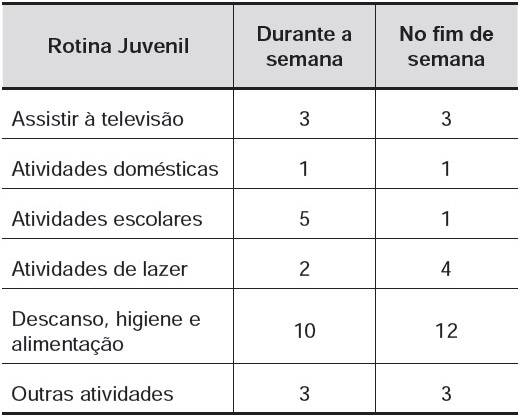
De acordo com esta pesquisa, quantas horas de seu tempo gasta um jovem entre 12 e 18 anos, na semana inteira (de segunda-feira a domingo), nas atividades escolares?
a) 20
b) 21
c) 24
d) 25
e) 27
Resposta: E
Gostou de saber um pouco mais sobre as expressões numéricas? Assim como tudo na matemática, esse conteúdo requer muita prática para ser dominado. Para ajudá-lo com esse e outros assuntos, preparamos um Plano de Estudos completíssimo com tudo o que você precisa para mandar super bem em suas provas!