
Gráficos: 3 dicas preciosas de como interpretar!
Vocês já estão craques em leitura e interpretação de gráficos? O Enem é uma prova que costuma abordar bastante esse tipo de conteúdo.
A Competência de área 6 em matemática do exame diz que os candidatos devem “interpretar informações de natureza científica e social obtidas da leitura de gráficos e tabelas…”. Em outras palavras: você precisa saber resolver questões que envolvem gráficos e tabelas.
Hoje, vamos apresentar os tipos de gráficos que costumam aparecer no exame e contar 3 dicas que podem te ajudar a encontrar a alternativa certa e evitar qualquer tipo de pegadinha.
O que são gráficos?
Gráficos são representações de dados por meio de recursos visuais, com o objetivo de destacar informações para que fique mais fácil a sua compreensão.
Normalmente, o gráfico é usado para cruzar informações e demonstrar desempenhos, como crescimento ou queda, por exemplo.
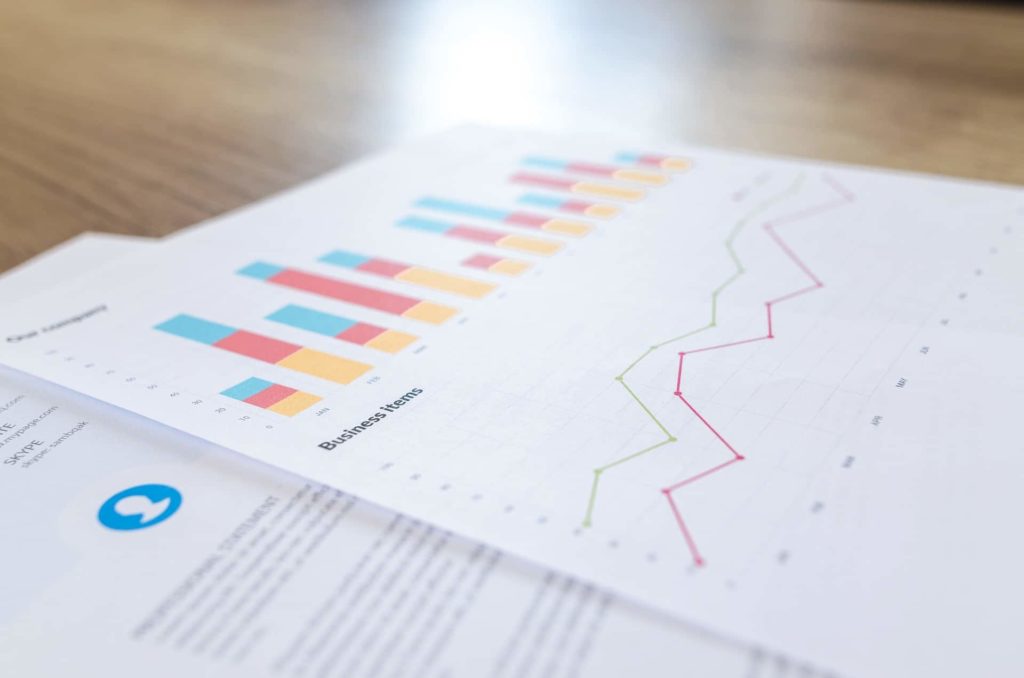
Os gráficos mais frequentes em vestibulares são: pizza, barras, colunas e linhas.
3 dicas para ler e interpretar gráficos
Agora que já sabemos o que são e como são, vamos ver o que pode nos ajudar na leitura e interpretação.
1. Confira se as informações do gráfico batem com as do enunciado do exercício
Muitas vezes esquecemos de nos atentar a essa parte e seguimos direto para o gráfico. O enunciado pode ter informações complementares que vão facilitar muito a resolução da questão.
Portanto, leia sempre e circule as informações principais.
2. Entenda qual tipo de informação está destacada no eixo vertical e qual está no eixo horizontal
Antes de analisar alguma informação, precisamos entender o gráfico como um todo. Veja o exemplo abaixo:

Esse gráfico foi usado numa questão de matemática do Enem de 2015. Ela está falando sobre a desvalorização de veículos após a sua compra.
No eixo vertical, temos a informação do preço que cada automóvel foi comprado. Já no eixo horizontal, temos a quantidade de anos que determinada pessoa ficou com o carro.
Só de observar as informações de cada eixo, já conseguimos identificar que a perda do carro Y foi muito maior, pois foi comprado a 55 mil reais e foi vendido a 10 mil, depois de 14 anos. Já o carro X, foi comprado a 30 mil reais e vendido a 15 mil.
No enunciado, a questão não fala o preço que ela comprou e vendeu o carro, mas a informação está explícita no gráfico.
3. Interprete com calma, pois geralmente as questões são contextualizadas
Se antes mesmo de você ler o gráfico, você já se assustou: relaxe! Normalmente, esse recurso é abordado de forma contextualizada, o que facilita sua resolução.
É muito comum conter dados estatísticos de pesquisas para eleições e outros temas presentes na vida dos cidadãos. Então, lembre-se que nem sempre será matemática pura. Nessas horas, é mais importante você pensar de forma lógica e resolver com calma a questão.
Gostou das nossas dicas? Então, não deixe de acessar nosso plano de estudos, lá você consegue personalizar seus estudos e se preparar para o Enem e vestibulares e ficar mais próximo de conseguir a vaga na faculdade dos sonhos!