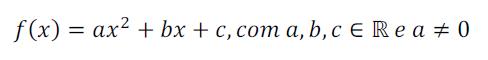
Função quadrática – Papel dos coeficientes no gráfico da função
No post de hoje vamos falar de função quadrática, passo a passo. As funções quadráticas, também chamadas de funções do 2º grau, são as funções que tem formato:
Gráfico da função quadrática
Os gráficos de funções quadráticas são sempre parábolas. Assim como em toda função, podemos plotar seu gráfico construindo uma tabela de pares (x,y), ou seja, atribuímos valores para x e calculamos seus y correspondentes, que são iguais a f(x).
Existe, porém, uma forma mais eficiente para fazer gráficos de funções do 2º grau. Apenas olhando a função já conseguimos tirar informações importantes sobre seu gráfico.
Os coeficientes da função vão determinar de forma direta o formato da parábola (concavidade pra cima ou pra baixo) e o ponto de intersecção com o eixo y. Coeficiente a O coeficiente a irá determinar se a parábola terá concavidade para cima ou para baixo.

Coeficiente c O coeficiente c vai determinar onde a parábola corta o eixo y, pois para x=0 temos f(x) = c.
Veja também os tópicos sobre função modular, entenda cada vez mais desse assunto tão cobrado nos vestibulares e teste seu aprendizado resolvendo exercícios de função quadrática.
